原文地址已失效
1、函数式编程思想概论
原文地址1
前言1
在讨论函数式编程(Functional Programming)的具体内容之前,我们首先看一下函数式编程的含义。在维基百科上,函数式编程的定义如下:”函数式编程是一种编程范式。它把计算当成是数学函数的求值,从而避免改变状态和使用可变数据。它是一种声明式的编程范式,通过表达式和声明而不是语句来编程。” (见 Functional Programming)
函数式编程的思想在软件开发领域由来已久。在众多的编程范式中,函数式编程虽然出现的时间很长,但是在编程范式领域和整个开发社区中的流行度一直不温不火。函数式编程有一部分狂热的支持者,在他们眼中,函数式编程思想是解决各种软件开发问题的终极方案;而另外的一部分人,则觉得函数式编程的思想并不容易理解,学习曲线较陡,上手起来也有一定的难度。大多数人更倾向于接受面向对象或是面向过程这样的编程范式。这也是造成函数式编程范式一直停留在小众阶段的原因。
这样两极化的反应,与函数式编程本身的特性是分不开的。函数式编程的思想脱胎于数学理论,也就是我们通常所说的λ演算( λ-calculus)。一听到数学理论,可能很多人就感觉头都大了。这的确是造成函数式编程的学习曲线较陡的一个原因。如同数学中的函数一样,函数式编程范式中的函数有独特的特性,也就是通常说的无状态或引用透明性(referential transparency)。一个函数的输出由且仅由其输入决定,同样的输入永远会产生同样的输出。这使得函数式编程在处理很多与状态相关的问题时,有着天然的优势。函数式编程的代码通常更加简洁,但是不一定易懂。函数式编程的解决方案中透露出优雅的美。
函数式编程所涵盖的内容非常广泛,从其背后的数学理论,到其中包含的基本概念,再到诸如 Haskell 这样的函数式编程语言,以及主流编程语言中对函数式编程方式的支持,相关的专有第三方库等。通过本系列的学习,你可以了解到很多函数式编程相关的概念。你会发现很多概念都可以在日常的开发中找到相应的映射。比如做前端的开发人员一定听说过高阶组件(high-order component),它就与函数式编程中的高阶函数有着异曲同工之妙。流行的前端状态管理方案 Redux 的核心是 reduce 函数。库 reselect 则是记忆化( memoization)的精妙应用。很多 Java 开发人员已经切实的体会到了 Java 8 中的 Lambda 表达式如何让对流(Stream)的操作变得简洁又自然。
近年来,随着多核平台和并发计算的发展,函数式编程的无状态特性,在处理这些问题时有着其他编程范式不可比拟的天然优势。不管是前端还是后端开发人员,学习一些函数式编程的思想和概念,对于手头的开发工作和以后的职业发展,都是大有裨益的。本系列虽然侧重的是 Java 平台上的函数式编程,但是对于其他背景的开发人员同样有借鉴意义。
下面介绍函数的基本概念。
函数1
我们先从数学中的函数开始谈起。数学中的函数是输入元素的集合到可能的输出元素的集合之间的映射关系,并且每个输入元素只能映射到一个输出元素。比如典型的函数 f(x)=xx 把所有实数的集合映射到其平方值的集合,如 f(2)=4 和 f(-2)=4。函数允许不同的输入元素映射到同一个输出元素,但是每个输入元素只能映射到一个输出元素。比如上述函数 f(x)=xx 中,2 和-2 都映射到同一个输出元素 4。这也限定了每个输入元素所对应的输出元素是固定的。每个输入元素都必须被映射到某个输出元素,也就是说函数可以应用到输入元素集合中的每个元素。
用专业的术语来说,输入元素称为函数的参数(argument)。输出元素称为函数的值(value)。输入元素的集合称为函数的定义域(domain)。输出元素和其他附加元素的集合称为函数的到达域(codomain)。存在映射关系的输入和输出元素对的集合,称为函数的图形(graph)。输出元素的集合称为像(image)。这里需要注意像和到达域的区别。到达域还可能包含除了像中元素之外的其他元素,也就是没有输入元素与之对应的元素。
图 1 表示了一个函数对应的映射关系(图片来源于维基百科上的 Function 条目)。输入集合 X 中的每个元素都映射到了输出集合 Y 中某个元素,即 f(1)=D、f(2)=C 和 f(3)=C。X 中的元素 2 和 3 都映射到了 Y 中的 C,这是合法的。Y 中的元素 B 和 A 没有被映射到,这也是合法的。该函数的定义域是 X,到达域是 Y,图形是 (1, D)、(2, C) 和 (3, C) 的集合,像是 C 和 D 的集合。
图 1. 函数的映射关系
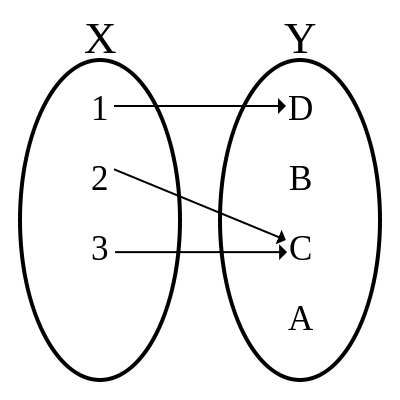
我们通常可以把函数看成是一个黑盒子,对其内部的实现一无所知。只需要清楚其映射关系,就可以正确的使用它。函数的图形是描述函数的一种方式,也就是列出来函数对应的映射中所有可能的元素对。这种描述方式用到了集合相关的理论,对于图 1 中这样的简单函数比较容易进行描述。对于包含输入变量的函数,如 f(x)=x+1,需要用到更加复杂的集合逻辑。因为输入元素 x 可以是任何数,定义域是一个无穷集合,对应的输出元素集合也是无穷的。要描述这样的函数,用我们下面介绍的 λ 演算会更加直观。
λ 演算
λ 演算是数理逻辑中的一个形式系统,在函数抽象和应用的基础上,使用变量绑定和替换来表达计算。讨论 λ 演算离不开形式化的表达。在本文中,我们尽量集中在与编程相关的基本概念上,而不拘泥于数学上的形式化表示。λ 演算实际上是对前面提到的函数概念的简化,方便以系统的方式来研究函数。λ 演算的函数有两个重要特征:
- λ 演算中的函数都是匿名的,没有显式的名称。比如函数
sum(x, y) = x + y可以写成(x, y)|-> x + y。由于函数本身仅由其映射关系来确定,函数名称实际上并没有意义。因此使用匿名函数是合理的。 - λ演算中的函数都只有一个输入。有多个输入的函数可以转换成多个只包含一个输入的函数的嵌套调用。这个过程就是通常所说的柯里化(currying)。如
(x, y)|-> x + y可以转换成x |-> (y |-> x + y)。右边的函数的返回值是另外一个函数。这一限定简化了λ演算的定义。
对函数简化之后,就可以开始定义 λ 演算。λ 演算是基于 λ 项(λ-term)的语言。λ 项是 λ 演算的基本单元。λ 演算在 λ 项上定义了各种转换规则。
λ项
λ 项由下面 3 个规则来定义:
- 一个变量 x 本身就是一个 λ 项。
- 如果 M 是 λ 项,x 是一个变量,那么 (λx.M) 也是一个 λ 项。这样的 λ 项称为 λ 抽象(abstraction)。x 和 M 中间的点(.)用来分隔函数参数和内容。
- 如果 M 和 N 都是 λ 项,那么 (MN) 也是一个 λ 项。这样的λ项称为应用(application)。
所有的合法 λ 项,都只能通过重复应用上面的 3 个规则得来。需要注意的是,λ 项最外围的括号是可以省略的,也就是可以直接写为 λx.M 和 MN。当多个 λ 项连接在一起时,需要用括号来进行分隔,以确定 λ 项的解析顺序。默认的顺序是左向关联的。所以 MNO 相当于 ((MN)O)。在不出现歧义的情况下,可以省略括号。
重复应用上述 3 个规则就可以得到所有的λ项。把变量作为λ项是重复应用规则的起点。λ 项 λx.M 定义的是匿名函数,把输入变量 x 的值替换到表达式 M 中。比如,λx.x+1 就是函数 f(x)=x+1 的 λ 抽象,其中 x 是变量,M 是 x+1。λ 项 MN 表示的是把表达式 N 应用到函数 M 上,也就是调用函数。N 可以是类似 x 这样的简单变量,也可以是 λ 抽象表示的项。当使用λ抽象时,就是我们通常所说的高阶函数的概念。
绑定变量和自由变量
在 λ 抽象中,如果变量 x 出现在表达式中,那么该变量被绑定。表达式中绑定变量之外的其他变量称为自由变量。我们可以用函数的方式来分别定义绑定变量(bound variable,BV)和自由变量(free variable,FV)。
对绑定变量来说:
- 对变量 x 来说,BV(x) = ∅。也就是说,一个单独的变量是自由的。
- 对 λ 项 M 和变量 x 来说,BV(λx.M) = BV(M) ∪ { x }。也就是说,λ 抽象在 M 中已有的绑定变量的基础上,额外绑定了变量 x。
- 对 λ 项 M 和λ项 N 来说,BV(MN) = BV(M) ∪ BV(N)。也就是说,λ 项的应用结果中的绑定变量的集合是各自 λ 项的绑定变量集合的并集。
对自由变量来说,相应的定义和绑定变量是相反的:
- 对变量 x 来说,FV(x) = { x }。
- 对 λ M 和变量 x 来说,FV(λx.M) = FV(M) − { x }。
- 对 λ 项 M 和 λ 项 N 来说,FV(MN) = FV(M) ∪ FV(N)。
在 λ 项 λx.x+1 中,x 是绑定变量,没有自由变量。在 λ 项 λx.x+y 中,x 是绑定变量,y 是自由变量。
在λ抽象中,绑定变量的名称在某些情况下是无关紧要的。如 λx.x+1 和 λy.y+1 实际上表示的是同样的函数,都是把输入值加 1。变量名称 x 或 y,并不影响函数的语义。类似 λx.x+1 和 λy.y+1 这样的 λ 项在λ演算中被认为是相等的,称为 α 等价(alpha equivalence)。
约简
在 λ 项上可以进行不同的约简(reduction)操作,主要有如下 3 种。
α 变换
α 变换(α-conversion)的目的是改变绑定变量的名称,避免名称冲突。比如,我们可以通过 α 变换把 λx.x+1 转换成 λy.y+1。如果两个λ项可以通过α变换来进行转换,则这两个 λ 项是 α 等价的。这也是我们上一节中提到的 α 等价的形式化定义。
对 λ 抽象进行 α 变换时,只能替换那些绑定到当前 λ 抽象上的变量。如 λ 抽象 λx.λx.x 可以 α 变换为 λx.λy.y 或 λy.λx.x,但是不能变换为 λy.λx.y,因为两者的语义是不同的。λx.x 表示的是恒等函数。λx.λx.x 和 λy.λx.x 都是表示返回恒等函数的 λ 抽象,因此它们是 α 等价的。而 λx.y 表示的不再是恒等函数,因此 λy.λx.y 与 λx.λy.y 和 λy.λx.x 都不是 α 等价的。
β 约简
β 约简(β-reduction)与函数应用相关。在讨论 β 约简之前,需要先介绍替换的概念。对于 λ 项 M 来说,M[x := N] 表示把 λ 项 M 中变量 x 的自由出现替换成 N。具体的替换规则如下所示。A、B 和 M 是 λ 项,而 x 和 y 是变量。A ≡ B 表示两个 λ 项是相等的。
- x[x := M] ≡ M:直接替换一个变量 x 的结果是用来进行替换的 λ 项 M。
- y[x := M] ≡ y(x ≠ y):y 是与 x 不同的变量,因此替换 x 并不会影响 y,替换结果仍然为 y。
- (AB)[x := M] ≡ (A[x := M]B[x := M]):A 和 B 都是 λ 项,(AB) 是 λ 项的应用。对 λ 项的应用进行替换,相当于替换之后再进行应用。
- (λx.A)[x := M] ≡ λx.A:这条规则针对 λ 抽象。如果 x 是 λ 抽象的绑定变量,那么不需要对 x 进行替换,得到的结果与之前的 λ 抽象相同。这是因为替换只是针对 M 中 x 的自由出现,如果 x 在 M 中是不自由的,那么替换就不需要进行。
- (λy.A)[x := M] ≡ λy.A[x := M](x ≠ y 并且 y ∉ FV(M)):这条规则也是针对λ抽象。λ 项 A 的绑定变量是 y,不同于要替换的 x,因此可以在 A 中进行替换动作。
在进行替换之前,可能需要先使用 α 变换来改变绑定变量的名称。比如,在进行替换 (λx.y)[y := x] 时,不能直接把出现的 y 替换成 x。这样就改变了之前的 λ 抽象的语义。正确的做法是先进行 α 变换,把 λx.y 替换成 λz.y,再进行替换,得到的结果是 λz.x。
替换的基本原则是要求在替换完成之后,原来的自由变量仍然是自由的。如果替换变量可能导致一个变量从自由变成绑定,需要首先进行 α 变换。在之前的例子中,λx.y 中的 x 是自由变量,而直接替换的结果 λx.x 把 x 变成了绑定变量,因此 α 变换是必须的。在正确的替换结果 λz.x 中,z 仍然是自由的。
β 约简用替换来表示函数应用。对 ((λV.E) E′) 进行 β 约简的结果就是 E[V := E′]。如 ((λx.x+1)y) 进行 β 约简的结果是 (x+1)[x := y],也就是 y+1。
η 变换
η 变换(η-conversion)描述函数的外延性(extensionality)。外延性指的是如果两个函数当且仅当对所有参数的结果相同时,才被认为是相等的。比如一个函数 F,当参数为 x 时,它的返回值是 Fx。那么考虑声明为 λy.Fy 的函数 G。函数 G 对于输入参数 x,同样返回结果 Fx。F 和 G 可能由不同的 λ 项组成,但是只要 Fx=Gx 对所有的 x 都成立,那么 F 和 G 是相等的。
以 F=λx.x 和 G=λx.(λy.y)x 来说,F 是恒等函数,而 G 则是在输入参数 x 上应用恒等函数。F 和 G 虽然由不同的 λ 项组成,但是它们的行为是一样,本质上都是恒等函数。我们称之为 F 和 G 是 η 等价的,F 是 G 的 η 约简,而 G 是 F 的 η 扩展。F 和 G 互为对方的 η 变换。
纯函数、副作用和引用透明性
了解函数式编程的人可能听说过纯函数和副作用等名称。这两个概念与引用透明性紧密相关。纯函数需要具备两个特征:
- 对于相同的输入参数,总是返回相同的值。
- 求值过程中不产生副作用,也就是不会对运行环境产生影响。
对于第一个特征,如果是从数学概念上抽象出来的函数,则很容易理解。比如 f(x)=x+1 和 g(x)=x*x 这样的函数,都是典型的纯函数。如果考虑到一般编程语言中出现的方法,则函数中不能使用静态局部变量、非局部变量,可变对象的引用或 I/O 流。这是因为这些变量的值可能在不同的函数执行中发生变化,导致产生不一样的输出。第二个特征,要求函数体中不能对静态局部变量、非局部变量,可变对象的引用或 I/O 流进行修改。这就保证了函数的执行过程中不会对外部环境造成影响。纯函数的这两个特征缺一不可。下面通过几个 Java 方法来具体说明纯函数。
在清单 1 中,方法 f1 是纯函数;方法 f2 不是纯函数,因为引用了外部变量 y;方法 f3 不是纯函数,因为使用了调用了产生副作用的 Counter 对象的 inc 方法;方法 f4 不是纯函数,因为调用 writeFile 方法会写入文件,从而对外部环境造成影响。
清单 1. 纯函数和非纯函数示例
int f1(int x) {
return x + 1;
}
int f2(int x) {
return x + y;
}
int f3(Counter c) {
c.inc();
return 0;
}
int f4(int x) {
writeFile();
return 1;
}
如果一个表达式是纯的,那么它在代码中的所有出现,都可以用它的值来代替。对于一个函数调用来说,这就意味着,对于同一个函数的输入参数相同的调用,都可以用其值来代替。这就是函数的引用透明性。引用透明性的重要性在于使得编译器可以用各种措施来对代码进行自动优化。
函数式编程与并发编程
随着计算机硬件多核的普及,为了尽可能地利用硬件平台的能力,并发编程显得尤为重要。与传统的命令式编程范式相比,函数式编程范式由于其天然的无状态特性,在并发编程中有着独特的优势。以 Java 平台来说,相信很多开发人员都对 Java 的多线程和并发编程有所了解。可能最直观的感受是,Java 平台的多线程和并发编程并不容易掌握。这主要是因为其中所涉及的概念太多,从 Java 内存模型,到底层原语 synchronized 和 wait/notify,再到 java.util.concurrent 包中的高级同步对象。由于并发编程的复杂性,即使是经验丰富的开发人员,也很难保证多线程代码不出现错误。很多错误只在运行时的特定情况下出现,很难排错和修复。在学习如何更好的进行并发编程的同时,我们可以从另外一个角度来看待这个问题。多线程编程的问题根源在于对共享变量的并发访问。如果这样的访问并不需要存在,那么自然就不存在多线程相关的问题。在函数式编程范式中,函数中并不存在可变的状态,也就不需要对它们的访问进行控制。这就从根本上避免了多线程的问题。
总结1
作为 Java 函数式编程系列的第一篇文章,本文对函数式编程做了简要的概述。由于函数式编程与数学中的函数密不可分,本文首先介绍了函数的基本概念。接着对作为函数式编程理论基础的λ演算进行了详细的介绍,包括λ项、自由变量和绑定变量、α变换、β约简和η变换等重要概念。最后介绍了编程中可能会遇到的纯函数、副作用和引用透明性等概念。本系列的下一篇文章将对函数式编程中的重要概念进行介绍,包括高阶函数、闭包、递归、记忆化和柯里化等。
参考资源1
2、函数式编程中的重要概念
原文地址2
前言2
本系列的上一篇文章对函数式编程思想进行了概述,本文将系统地介绍函数式编程中的常见概念。这些概念对大多数开发人员来说可能并不陌生,在日常的编程实践中也比较常见。
函数式编程范式的意义
在众多的编程范式中,大多数开发人员比较熟悉的是面向对象编程范式。一方面是由于面向对象编程语言比较流行,与之相关的资源比较丰富;另外一方面是由于大部分学校和培训机构的课程设置,都选择流行的面向对象编程语言。面向对象编程范式的优点在于其抽象方式与现实中的概念比较相近。比如,学生、课程、汽车和订单等这些现实中的概念,在抽象成相应的类之后,我们很容易就能理解类之间的关联关系。这些类中所包含的属性和方法可以很直观地设计出来。举例来说,学生所对应的类 Student 就应该有姓名、出生日期和性别等基本的属性,有方法可以获取到学生的年龄、所在的班级等信息。使用面向对象的编程思想,可以直观地在程序要处理的问题和程序本身之间,建立直接的对应关系。这种从问题域到解决域的简单对应关系,使得代码的可读性很强。对于初学者来说,这极大地降低了上手的难度。
函数式编程范式则相对较难理解。这主要是由于函数所代表的是抽象的计算,而不是具体的实体。因此比较难通过类比的方式来理解。举例来说,已知直角三角形的两条直角边的长度,需要通过计算来得到第三条边的长度。这种计算方式可以使用函数来表示。length(a, b)=√a²+b² 就是具体的计算方式。这样的计算方式与现实中的实体没有关联。
基于计算的抽象方式可以进一步提高代码的复用性。在一个学生信息管理系统中,可能会需要找到一个班级的某门课程的最高分数;在一个电子商务系统中,也可能会需要计算一个订单的总金额。看似风马牛不相及的两件事情,其实都包含了同样的计算在里面。也就是对一个可迭代的对象进行遍历,同时在遍历的过程中执行自定义的操作。在计算最高分数的场景中,在遍历的同时需要保存当前已知最高分数,并在遍历过程中更新该值;在计算订单总金额的场景中,在遍历的同时需要保存当前已累积的金额,并在遍历过程中更新该值。如果用 Java 代码来实现,可以很容易写出如下两段代码。清单 1 计算学生的最高分数。
清单 1. 计算学生的最高分数的代码
int maxMark = 0;
for (Student student : students) {
if (student.getMark() > maxMark) {
maxMark = student.getMark();
}
}
清单 2 计算订单的总金额。
清单 2. 计算订单的总金额的代码
BigDecimal total = BigDecimal.ZERO;
for (LineItem item : order.getLineItems()) {
total = total.add(item.getPrice().multiply(new BigDecimal(item.getCount())));
}
在面向对象编程的实现中,这两段代码会分别添加到课程和订单所对应的类的某个方法中。课程对应的类 Course 会有一个方法叫 getMaxMark,而订单对应的类 Order 会有一个方法叫 getTotal。尽管在实现上存在很多相似性和重复代码,由于课程和订单是两个完全不相关的概念,并没有办法通过面向对象中的继承或组合机制来提高代码复用和减少重复。而函数式编程可以很好地解决这个问题。
我们来进一步看一下清单 1 和清单 2 中的代码,尝试提取其中的计算模式。该计算模式由 3 个部分组成:
- 保存计算结果的状态,有初始值。
- 遍历操作。
- 遍历时进行的计算,更新保存计算结果的状态值。
把这 3 个元素提取出来,用伪代码表示,就得到了清单 3 中用函数表示的计算模式。iterable 表示被迭代的对象,updateValue 是遍历时进行的计算,initialValue 是初始值。
清单 3. 计算模式的伪代码
function(iterable, updateValue, initialValue) {
value = initialValue
loop(iterable) {
value = updateValue(value, currentValue)
}
return value
}
了解函数式编程的读者应该已经看出来了,这就是常用的 reduce 函数。使用 reduce 对清单 1 和清单 2 进行改写,可以得到清单 4 中的两段新的代码。
清单 4. 使用 reduce 函数改写代码
reduce(students, (mark, student) -> {
return Math.max(student.getMark(), mark);
}, 0);
reduce(order.lineItems, (total, item) -> {
return total.add(item.getPrice().multiply(new BigDecimal(item.getCount())))
}, BigDecimal.ZERO);
函数类型与高阶函数
对函数式编程支持程度高低的一个重要特征是函数是否作为编程语言的一等公民出现,也就是编程语言是否有内置的结构来表示函数。作为面向对象的编程语言,Java 中使用接口来表示函数。直到 Java 8,Java 才提供了内置标准 API 来表示函数,也就是 java.util.function 包。Function<T, R> 表示接受一个参数的函数,输入类型为 T,输出类型为 R。Function 接口只包含一个抽象方法 R apply(T t),也就是在类型为 T 的输入 t 上应用该函数,得到类型为 R 的输出。除了接受一个参数的 Function 之外,还有接受两个参数的接口 BiFunction<T, U, R>,T 和 U 分别是两个参数的类型,R 是输出类型。BiFunction 接口的抽象方法为 R apply(T t, U u)。超过 2 个参数的函数在 Java 标准库中并没有定义。如果函数需要 3 个或更多的参数,可以使用第三方库,如 Vavr 中的 Function0 到 Function8。
除了 Function 和 BiFunction 之外,Java 标准库还提供了几种特殊类型的函数:
Consumer<T>:接受一个输入,没有输出。抽象方法为 void accept(T t)。Supplier<T>:没有输入,一个输出。抽象方法为 T get()。Predicate<T>:接受一个输入,输出为 boolean 类型。抽象方法为 boolean test(T t)。UnaryOperator<T>:接受一个输入,输出的类型与输入相同,相当于Function<T, T>。BinaryOperator<T>:接受两个类型相同的输入,输出的类型与输入相同,相当于BiFunction<T,T,T>。BiPredicate<T, U>:接受两个输入,输出为 boolean 类型。抽象方法为 boolean test(T t, U u)。
在本系列的第一篇文章中介绍 λ 演算时,提到了高阶函数的概念。λ 项在定义时就支持以 λ 项进行抽象和应用。具体到实际的函数来说,高阶函数以其他函数作为输入,或产生其他函数作为输出。高阶函数使得函数的组合成为可能,更有利于函数的复用。熟悉面向对象的读者对于对象的组合应该不陌生。在划分对象的职责时,组合被认为是优于继承的一种方式。在使用对象组合时,每个对象所对应的职责单一。多个对象通过组合的方式来完成复杂的行为。函数的组合类似对象的组合。上一节中提到的 reduce 就是一个高阶函数的示例,其参数 updateValue 也是一个函数。通过组合,reduce 把一部分逻辑代理给了作为其输入的函数 updateValue。不同的函数的嵌套层次可以很多,完成复杂的组合。
在 Java 中,可以使用函数类型来定义高阶函数。上述函数接口都可以作为方法的参数和返回值。Java 标准 API 已经大量使用了这样的方式。比如 Iterable 的 forEach 方法就接受一个 Consumer 类型的参数。
在清单 5 中,notEqual 返回值是一个 Predicate 对象,并使用在 Stream 的 filter 方法中。代码运行的输出结果为 2 和 3。
清单 5. 高阶函数示例
public class HighOrderFunctions {
private static <T> Predicate<T> notEqual(T t) {
return (v) -> !Objects.equals(v, t);
}
public static void main(String[] args) {
List.of(1, 2, 3)
.stream()
.filter(notEqual(1))
.forEach(System.out::println);
}
}
部分函数
部分函数(partial function)是指仅有部分输入参数被绑定了实际值的函数。清单 6 中的函数 f(a, b, c) = a + b +c 有 3 个参数 a、b 和 c。正常情况下调用该函数需要提供全部 3 个参数的值。如果只提供了部分参数的值,如只提供了 a 值,就得到了一个部分函数,其中参数 a 被绑定成了给定值。假设给定的参数 a 的值是 1,那新的部分函数的定义是 fa(b, c) = 1 + b + c。由于 a 的实际值可以有无穷多,也有对应的无穷多种可能的部分函数。除了只对 a 绑定值之外,还可以绑定参数 b 和 c 的值。
清单 6. 部分函数示例
function f(a, b, c) {
return a + b + c;
}
function fa(b, c) {
return f(1, b, c);
}
部分函数可以用来为函数提供快捷方式,也就是预先绑定一些常用的参数值。比如函数 add(a, b) = a + b 用来对 2 个参数进行相加操作。可以在 add 基础上创建一个部分函数 increase,把参数 b 的值绑定为 1。increase 相当于进行加 1 操作。同样的,把参数值 b 绑定为 -1 可以得到函数 decrease。
Java 标准库并没有提供对部分函数的支持,而且由于只提供了 Function 和 BiFunction,部分函数只对 BiFunction 有意义。不过我们可以自己实现部分函数。部分函数在绑定参数时有两种方式:一种是按照从左到右的顺序绑定参数,另外一种是按照从右到左的顺序绑定参数。这两个方式分别对应于 清单 7 中的 partialLeft 和 partialRight 方法。这两个方法把一个 BiFunction 转换成一个 Function。
清单 7. 部分函数的 Java 实现
public class PartialFunctions {
private static <T, U, R> Function<U, R> partialLeft(BiFunction<T, U, R> biFunction, T t) {
return (u) -> biFunction.apply(t, u);
}
private static <T, U, R> Function<T, R> partialRight(BiFunction<T, U, R> biFunction, U u) {
return (t) -> biFunction.apply(t, u);
}
public static void main(String[] args) {
BiFunction<Integer, Integer, Integer> biFunction = (v1, v2) -> v1 - v2;
Function<Integer, Integer> subtractFrom10 = partialLeft(biFunction, 10);
Function<Integer, Integer> subtractBy10 = partialRight(biFunction, 10);
System.out.println(subtractFrom10.apply(5)); // 5
System.out.println(subtractBy10.apply(5)); // -5
}
}
柯里化
柯里化(currying)是与λ演算相关的重要概念。通过柯里化,可以把有多个输入的函数转换成只有一个输入的函数,从而可以在λ演算中来表示。柯里化的名称来源于数学家 Haskell Curry。Haskell Curry 是一位传奇性的人物,以他的名字命令了 3 种编程语言,Haskell、Brook 和 Curry。柯里化是把有多个输入参数的求值过程,转换成多个只包含一个参数的函数的求值过程。对于清单 6 的函数 f(a, b, c),在柯里化之后转换成函数 g,则对应的调用方式是 g(a)(b)(c)。函数 (x, y) -> x + y 经过柯里化之后的结果是 x -> (y -> x + y)。
柯里化与部分函数存在一定的关联,但两者是有区别的。部分函数的求值结果永远是实际的函数调用结果;而柯里化函数的求值结果则可能是另外一个函数。以清单 6 的部分函数 fa 为例,每次调用 fa 时都必须提供剩余的 2 个参数。求值的结果都是具体的值;而调用柯里化之后的函数 g(a) 得到的是另外的一个函数。只有通过递归的方式依次求值之后,才能得到最终的结果。
闭包
闭包(closure)是函数式编程相关的一个重要概念,也是很多开发人员比较难以理解的概念。很多编程语言都有闭包或类似的概念。
在上一篇文章介绍 λ 演算的时候提到过 λ 项的自由变量和绑定变量,如 λx.x+y 中的 y 就是自由变量。在对λ项求值时,需要一种方式可以获取到自由变量的实际值。由于自由变量不在输入中,其实际值只能来自于执行时的上下文环境。实际上,闭包的概念来源于 1960 年代对 λ 演算中表达式求值方式的研究。
闭包的概念与高阶函数密切相关。在很多编程语言中,函数都是一等公民,也就是存在语言级别的结构来表示函数。比如 Python 中就有函数类型,JavaScript 中有 function 关键词来创建函数。对于这样的语言,函数可以作为其他函数的参数,也可以作为其他函数的返回值。当一个函数作为返回值,并且该函数内部使用了出现在其所在函数的词法域(lexical scope)的自由变量时,就创建了一个闭包。我们首先通过一段简单的 JavaScript 代码来直观地了解闭包。
清单 8 中的函数 idGenerator 用来创建简单的递增式的 ID 生成器。参数 initialValue 是递增的初始值。返回值是另外一个函数,在调用时会返回并递增 count 的值。这段代码就用到了闭包。idGenerator 返回的函数中使用了其所在函数的词法域中的自由变量 count。count 不在返回的函数中定义,而是来自包含该函数的词法域。在实际调用中,虽然 idGenerator 函数的执行已经结束,其返回的函数 genId 却仍然可以访问 idGenerator 词法域中的变量 count。这是由闭包的上下文环境提供的。
清单 8. JavaScript 中的闭包示例
function idGenerator(initialValue) {
let count = initialValue;
return function() {
return count++;
};
}
let genId = idGenerator(0);
genId(); // 0
genId(); // 1
从上述简单的例子中,可以得出来构成闭包的两个要件:
- 一个函数
- 负责绑定自由变量的上下文环境
函数是闭包对外的呈现部分。在闭包创建之后,闭包的存在与否对函数的使用者是透明的。比如清单 8 中的 genId 函数,使用者只需要调用即可,并不需要了解背后是否有闭包的存在。上下文环境则是闭包背后的实现机制,由编程语言的运行时环境来提供。该上下文环境需要为函数创建一个映射,把函数中的每个自由变量与闭包创建时的对应值关联起来,使得闭包可以继续访问这些值。在 idGenerator 的例子中,上下文环境负责关联变量 count 的值,该变量可以在返回的函数中继续访问和修改。
从上述两个要件也可以得出闭包这个名字的由来。闭包是用来封闭自由变量的,适合用来实现内部状态。比如清单 8 中的 count 是无法被外部所访问的。一旦 idGenerator 返回之后,唯一的引用就来自于所返回的函数。在 JavaScript 中,闭包可以用来实现真正意义上的私有变量。
从闭包的使用方式可以得知,闭包的生命周期长于创建它的函数。因此,自由变量不能在堆栈上分配;否则一旦函数退出,自由变量就无法继续访问。因此,闭包所访问的自由变量必须在堆上分配。也正因为如此,支持闭包的编程语言都有垃圾回收机制,来保证闭包所访问的变量可以被正确地释放。同样,不正确地使用闭包可能造成潜在的内存泄漏。
闭包的一个重要特性是其中的自由变量所绑定的是闭包创建时的值,而不是变量的当前值。清单 9 是一个简单的 HTML 页面的代码,其中有 3 个按钮。用浏览器打开该页面时,点击 3 个按钮会发现,所弹出的值全部都是 3。这是因为当点击按钮时,循环已经执行完成,i 的当前值已经是 3。所以按钮的 click 事件处理函数所得到是 i 的当前值 3。
清单 9. 闭包绑定值的演示页面
<!DOCTYPE html>
<html lang="en">
<head>
<title>Test</title>
</head>
<body>
<button>Button 1</button>
<button>Button 2</button>
<button>Button 3</button>
</body>
<script>
var buttons = document.getElementsByTagName("button");
for (var i = 0; i < buttons.length; i++) {
buttons[i].addEventListener("click", function() {
alert(i);
});
}
</script>
</html>
如果把 JavaScript 代码改成清单 10 所示,就可以得到所期望的结果。我们创建了一个匿名函数并马上调用该函数来返回真正的事件处理函数。处理函数中访问的变量 i 现在成为了闭包的自由变量,因此 i 的值被绑定到闭包创建时的值,也就是每个循环执行过程中的实际值。
清单 10. 使用闭包解决绑定值的问题
var buttons = document.getElementsByTagName("button");
for (var i = 0; i < buttons.length; i++) {
buttons[i].addEventListener("click", function(i) {
return function() {
alert(i);
}
}(i));
}
在 Java 中有与闭包类似的概念,那就是匿名内部类。在匿名内部类中,可以访问词法域中声明为 final 的变量。不是 final 的变量无法被访问,会出现编译错误。匿名内部类提供了一种方式来共享局部变量。不过并不能对该变量的引用进行修改。在清单 11 中,变量 latch 被两个匿名内部类所使用。
清单 11. Java 中的匿名内部类
public class InnerClasses {
public static void main(String[] args) {
final CountDownLatch latch = new CountDownLatch(1);
final Future<?> task1 = ForkJoinPool.commonPool().submit(() -> {
try {
Thread.sleep(ThreadLocalRandom.current().nextInt(2000));
} catch (InterruptedException e) {
e.printStackTrace();
} finally {
latch.countDown();
}
});
final Future<?> task2 = ForkJoinPool.commonPool().submit(() -> {
final long start = System.currentTimeMillis();
try {
latch.await();
} catch (InterruptedException e) {
e.printStackTrace();
} finally {
System.out.println("Done after " + (System.currentTimeMillis() - start) + "ms");
}
});
try {
task1.get();
task2.get();
} catch (InterruptedException | ExecutionException e) {
e.printStackTrace();
}
}
}
可以被共享的变量必须声明为 final。这个限制只对变量引用有效。只要对象本身是可变的,仍然可以修改该对象的内容。比如一个 List 类型的变量,虽然对它的引用是 final 的,仍然可以通过其方法来修改 List 内部的值。
递归
递归(recursion)是编程中的一个重要概念。很多编程语言,不仅限于函数式编程语言,都有递归这样的结构。从代码上来说,递归允许一个函数在其内部调用该函数自身。有些函数式编程语言并没有循环这样的结构,而是通过递归来实现循环。递归和循环在表达能力上是相同的,只不过命令式编程语言偏向于使用循环,而函数式编程语言偏向于使用递归。递归的优势在于天然适合于那些需要用分治法(divide and conquer)解决的问题,把一个大问题划分成小问题,以递归的方式解决。经典的通过递归解决的问题包括阶乘计算、计算最大公约数的欧几里德算法、汉诺塔、二分查找、树的深度优先遍历和快速排序等。
递归分为单递归和多递归。单递归只包含一个对自身的引用;而多递归则包含多个对自身的引用。单递归的例子包括列表遍历和计算阶乘等;多递归的例子包括树遍历等。在具体的编程实践中,单递归可以比较容易改写成使用循环的形式,而多递归则一般保持递归的形式。清单 12 给出了 JavaScript 实现的计算阶乘的递归写法。
清单 12. 递归方式计算阶乘
int fact(n) {
if (n === 0) {
return 1;
} else {
return n * fact(n - 1);
}
}
而下面的清单 13 则是 JavaScript 实现的使用循环的写法。
清单 13. 循环方式计算阶乘
int fact_i(n) {
let result = 1;
for (let i = n; i > 0; i--) {
result = result * i;
}
return result;
}
有一种特殊的递归方式叫尾递归。如果函数中的递归调用都是尾调用,则该函数是尾递归函数。尾递归的特性使得递归调用不需要额外的空间,执行起来也更快。不少编程语言会自动对尾递归进行优化。
下面我们以欧几里德算法来说明一下尾递归。该算法的 Java 实现比较简单,如清单 14 所示。函数 gcd 的尾调用是递归调用 gcd 本身。
清单 14. 尾递归的方式实现欧几里德算法
int gcd(x, y) {
if (y == 0) {
return x;
}
return gcd(y, x % y);
}
尾递归的特性在于实现时可以复用函数的当前调用栈的帧。当函数执行到尾调用时,只需要简单的 goto 语句跳转到函数开头并更新参数的值即可。相对于循环,递归的一个大的问题是层次过深的函数调用栈导致占用内存空间过大。对尾递归的优化,使得递归只需要使用与循环相似大小的内存空间。
记忆化
记忆化(memoization)也是函数式编程中的重要概念,其核心思想是以空间换时间,提高函数的执行性能,尤其是使用递归来实现的函数。使用记忆化要求函数具有引用透明性,从而可以把函数的调用结果与调用时的参数关联起来。通常是做法是在函数内部维护一个查找表。查找表的键是输入的参数,对应的值是函数的返回结果。在每次调用时,首先检查内部的查找表,如果存在与输入参数对应的值,则直接返回已经记录的值。否则的话,先进行计算,再用得到的值更新查找表。通过这样的方式可以避免重复的计算。
最典型的展示记忆化应用的例子是计算斐波那契数列 (Fibonacci sequence)。该数列的表达式是 F[n]=F[n-1]+F[n-2](n>=2,F[0]=0,F[1]=1)。清单 15 是斐波那契数列的一个简单实现,直接体现了斐波那契数列的定义。函数 fib 可以正确完成数列的计算,但是性能极差。当输入 n 的值稍微大一些的时候,计算速度就非常之慢,甚至会出现无法完成的情况。这是因为里面有太多的重复计算。比如在计算 fib(4) 的时候,会计算 fib(3) 和 fib(2)。在计算 fib(3) 的时候,也会计算 fib(2)。由于 fib 函数的返回值仅由参数 n 决定,当第一次得出某个 n 对应的结果之后,就可以使用查找表把结果保存下来。这里需要使用 BigInteger 来表示值,因为 fib 函数的值已经超出了 Long 所能表示的范围。
清单 15. 计算斐波那契数列的朴素实现
import java.math.BigInteger;
public class Fib {
public static void main(String[] args) {
System.out.println(fib(40));
}
private static BigInteger fib(int n) {
if (n == 0) {
return BigInteger.ZERO;
} else if (n == 1) {
return BigInteger.ONE;
}
return fib(n - 1).add(fib(n - 2));
}
}
清单 16 是使用记忆化之后的计算类 FibMemoized。已经计算的值保存在查找表 lookupTable 中。每次计算之前,首先查看查找表中是否有值。改进后的函数的性能有了数量级的提升,即便是 fib(100) 也能很快完成。
清单 16. 使用记忆化的斐波那契数列计算
import java.math.BigInteger;
import java.util.HashMap;
import java.util.Map;
public class FibMemoized {
public static void main(String[] args) {
System.out.println(fib(100));
}
private static Map<Integer, BigInteger> lookupTable = new HashMap<>();
static {
lookupTable.put(0, BigInteger.ZERO);
lookupTable.put(1, BigInteger.ONE);
}
private static BigInteger fib(int n) {
if (lookupTable.containsKey(n)) {
return lookupTable.get(n);
} else {
BigInteger result = fib(n - 1).add(fib(n - 2));
lookupTable.put(n, result);
return result;
}
}
}
很多函数式编程库都提供了对记忆化的支持,会在本系列后续的文章中介绍。
总结2
本文对函数式编程相关的一些重要概念做了系统性介绍。理解这些概念可以为应用函数式编程实践打下良好的基础。本文首先介绍了函数式编程范式的意义,接着介绍了函数类型与高阶函数、部分函数、柯里化、闭包、递归和记忆化等概念。下一篇文章将介绍 Java 8 所引入的 Lambda 表达式和流处理。
参考资源2
3、Java 8的Lambda表达式和流处理
原文地址3
前言3
在本系列的前两篇文章中,已经对函数式编程的思想和函数式编程的重要概念做了介绍。本文将介绍 Java 平台本身对函数式编程的支持,着重介绍 Lambda 表达式和流(Stream)。
Lambda 表达式
当提到 Java 8 的时候,Lambda 表达式总是第一个提到的新特性。Lambda 表达式把函数式编程风格引入到了 Java 平台上,可以极大的提高 Java 开发人员的效率。这也是 Java 社区期待已久的功能,已经有很多的文章和图书讨论过 Lambda 表达式。本文则是基于官方的 JSR 335(Lambda Expressions for the Java Programming Language)来从另外一个角度介绍 Lambda 表达式。
引入 Lambda 表达式的动机
我们先从清单 1 中的代码开始谈起。该示例的功能非常简单,只是启动一个线程并输出文本到控制台。虽然该 Java 程序一共有 9 行代码,但真正有价值的只有其中的第 5 行。剩下的代码全部都是为了满足语法要求而必须添加的冗余代码。代码中的第 3 到第 7 行,使用 java.lang.Runnable 接口的实现创建了一个新的 java.lang.Thread 对象,并调用 Thread 对象的 start 方法来启动它。Runnable 接口是通过一个匿名内部类实现的。
清单 1. 传统的启动线程的方式
public class OldThread {
public static void main(String[] args) {
new Thread(new Runnable() {
public void run() {
System.out.println("Hello World!");
}
}).start();
}
}
从简化代码的角度出发,第 3 行和第 7 行的 new Runnable() 可以被删除,因为接口类型 Runnable 可以从类 Thread 的构造方法中推断出来。第 4 和第 6 行同样可以被删除,因为方法 run 是接口 Runnable 中的唯一方法。把第 5 行代码作为 run 方法的实现不会出现歧义。把第 3,4,6 和 7 行的代码删除掉之后,就得到了使用 Lambda 表达式的实现方式,如清单 2 所示。只用一行代码就完成了清单 1 中 5 行代码完成的工作。这是令人兴奋的变化。更少的代码意味着更高的开发效率和更低的维护成本。这也是 Lambda 表达式深受欢迎的原因。
清单 2. 使用 Lambda 表 达式启动线程
public class LambdaThread {
public static void main(String[] args) {
new Thread(() -> System.out.println("Hello World!")).start();
}
}
简单来说,Lambda 表达式是创建匿名内部类的语法糖(syntax sugar)。在编译器的帮助下,可以让开发人员用更少的代码来完成工作。
函数式接口
在对清单 1 的代码进行简化时,我们定义了两个前提条件。第一个前提是要求接口类型,如示例中的 Runnable,可以从当前上下文中推断出来;第二个前提是要求接口中只有一个抽象方法。如果一个接口仅有一个抽象方法(除了来自 Object 的方法之外),它被称为函数式接口(functional interface)。函数式接口的特别之处在于其实例可以通过 Lambda 表达式或方法引用来创建。Java 8 的 java.util.function 包中添加了很多新的函数式接口。如果一个接口被设计为函数式接口,应该添加@FunctionalInterface 注解。编译器会确保该接口确实是函数式接口。当尝试往该接口中添加新的方法时,编译器会报错。
目标类型
Lambda 表达式没有类型信息。一个 Lambda 表达式的类型由编译器根据其上下文环境在编译时刻推断得来。举例来说,Lambda 表达式 () -> System.out.println(“Hello World!”) 可以出现在任何要求一个函数式接口实例的上下文中,只要该函数式接口的唯一方法不接受任何参数,并且返回值是 void。这可能是 Runnable 接口,也可能是来自第三方库或应用代码的其他函数式接口。由上下文环境所确定的类型称为目标类型。Lambda 表达式在不同的上下文环境中可以有不同的类型。类似 Lambda 表达式这样,类型由目标类型确定的表达式称为多态表达式(poly expression)。
Lambda 表达式的语法很灵活。它们的声明方式类似 Java 中的方法,有形式参数列表和主体。参数的类型是可选的。在不指定类型时,由编译器通过上下文环境来推断。Lambda 表达式的主体可以返回值或 void。返回值的类型必须与目标类型相匹配。当 Lambda 表达式的主体抛出异常时,异常的类型必须与目标类型的 throws 声明相匹配。
由于 Lambda 表达式的类型由目标类型确定,在可能出现歧义的情况下,可能有多个类型满足要求,编译器无法独自完成类型推断。这个时候需要对代码进行改写,以帮助编译器完成类型推断。一个常见的做法是显式地把 Lambda 表达式赋值给一个类型确定的变量。另外一种做法是显示的指定类型。
在清单 3 中,函数式接口 A 和 B 分别有方法 a 和 b。两个方法 a 和 b 的类型是相同的。类 UseAB 的 use 方法有两个重载形式,分别接受类 A 和 B 的对象作为参数。在方法 targetType 中,如果直接使用 () -> System.out.println(“Use”) 来调用 use 方法,会出现编译错误。这是因为编译器无法推断该 Lambda 表达式的类型,类型可能是 A 或 B。这里通过显式的赋值操作为 Lambda 表达式指定了类型 A,从而可以编译通过。
清单 3. 可能出现歧义的目标类型
public class LambdaTargetType {
@FunctionalInterface
interface A {
void a();
}
@FunctionalInterface
interface B {
void b();
}
class UseAB {
void use(A a) {
System.out.println("Use A");
}
void use(B b) {
System.out.println("Use B");
}
}
void targetType() {
UseAB useAB = new UseAB();
A a = () -> System.out.println("Use");
useAB.use(a);
}
}
名称解析
在 Lambda 表达式的主体中,经常需要引用来自包围它的上下文环境中的变量。Lambda 表达式使用一个简单的策略来处理主体中的名称解析问题。Lambda 表达式并没有引入新的命名域(scope)。Lambda 表达式中的名称与其所在上下文环境在同一个词法域中。Lambda 表达式在执行时,就相当于是在包围它的代码中。在 Lambda 表达式中的 this 也与包围它的代码中的含义相同。在清单 4 中,Lambda 表达式的主体中引用了来自包围它的上下文环境中的变量 name。
清单 4. Lambda 表 达式中的名称解析
public void run() {
String name = "Alex";
new Thread(() -> System.out.println("Hello, " + name)).start();
}
需要注意的是,可以在 Lambda 表达式中引用的变量必须是声明为 final 或是实际上 final(effectively final)的。实际上 final 的意思是变量虽然没有声明为 final,但是在初始化之后没有被赋值。因此变量的值没有改变。
流
Java 8 中的流表示的是元素的序列。流中的元素可能是对象、int、long 或 double 类型。流作为一个高层次的抽象,并不关注流中元素的来源或是管理方式。流只关注对流中元素所进行的操作。当流与函数式接口和 Lambda 表达式一同使用时,可以写出简洁高效的数据处理代码。下面介绍几个与流相关的基本概念。
顺序执行和 并行执行
流的操作可以顺序执行或并行执行, 后者可以获得比前者更好的性能。但是如果实现不当,可能由于数据竞争或无用的线程同步,导致并行执行时的性能更差。一个流是否会并行执行,可以通过其方法 isParallel() 来判断。根据流的创建方式,一个流有其默认的执行方式。可以使用方法 sequential() 或 parallel() 来将其执行方式设置为顺序或并行。
相遇顺序
一个流的相遇顺序(encounter order)是流中的元素被处理时的顺序。流根据其特征可能有,也可能没有一个确定的相遇顺序。举例来说,从 ArrayList 创建的流有确定的相遇顺序;从 HashSet 创建的流没有确定的相遇顺序。大部分的流操作会按照流的相遇顺序来依次处理元素。如果一个流是无序的,同一个流处理流水线在多次执行时可能产生不一样的结果。比如 Stream 的 findFirst() 方法获取到流中的第一个元素。如果在从 ArrayList 创建的流上应用该操作,返回的总是第一个元素;如果是从 HashSet 创建的流,则返回的结果是不确定的。对于一个无序的流,可以使用 sorted 操作来排序;对于一个有序的流,可以使用 unordered() 方法来使其无序。
Spliterator
所有的流都是从 Spliterator 创建出来的。Spliterator 的名称来源于它所支持的两种操作:split 和 iterator。Spliterator 可以看成是 Iterator 的并行版本,允许通过对流中元素分片的方式来切分数据源。使用其 tryAdvance 方法来顺序遍历元素,也可以使用 trySplit 方法来创建一个新的 Spliterator 对象在新划分的数据集上工作。Spliterator 还提供了 forEachRemaining 方法进行批量顺序遍历。可以使用 estimateSize 方法来查询可能会遍历的元素数量。一般的做法是先使用 trySplit 切分数据源。当元素数量足够小时,使用 forEachRemaining 来对分片中的全部元素进行处理。这也是典型的分治法的思路。
每个 Spliterator 可以有一系列不同的特征,可以通过 characteristics 方法来查询。一个 Spliterator 具备的特征取决于其数据源和元素。所有可用的特征如下所示:
- CONCURRENT:表明数据源可以安全地由多个线程进行修改,而无需额外的同步机制。
- DISTINCT:表明数据源中的元素是唯一的,不存在重复元素。
- IMMUTABLE:表明数据源是不可变的, 无法进行修改操作。
- NONNULL:表明数据源中不存在 null 元素。
- ORDERED:表明数据源中的元素有确定的相遇顺序。
- SIZED:表明数据源中的元素的数量是确定的。
- SORTED:表明数据源中的元素是有序的。
- SUBSIZED:表明使用 trySplit 切分出来的子数据源也有 SIZED 和 SUBSIZED 的特征。
Spliterator 需要绑定到流之后才能遍历其中的元素。不同的 Spliterator 实现可能有不同的绑定时机。如果一个 Spliterator 是延迟绑定的,那么只有在进行首次遍历、首次切分或首次查询大小时,才会绑定到流上;反之,它会在创建时或首次调用任何方法时绑定到流上。绑定时机的重要性在于,在绑定之前对流所做的修改,在 Spliterator 遍历时是可见的。延迟绑定可以提供最大限度的灵活性。
有状态和无状态操作
流操作可以是有状态或无状态的。当一个有状态的操作在处理一个元素时,它可能需要使用处理之前的元素时保留的信息;无状态的操作可以独立处理每个元素,举例来说:
- distinct 和 sorted 是有状态操作的例子。distinct 操作从流中删除重复元素,它需要记录下之前已经遇到过的元素来确定当前元素是否应该被删除。sorted 操作对流进行排序,它需要知道所有元素来确定当前元素在排序之后的所在位置。
- filter 和 map 是无状态操作的例子。filter 操作在进行过滤时只需要看当前元素即可。map 操作可以独立转换当前元素。一般来说,有状态操作的运行代价要高于无状态操作,因为需要额外的空间保存中间状态信息。
Stream<T> 是表示流的接口,T 是流中元素的类型。对于原始类型的流,可以使用专门的类 IntStream、LongStream 和 DoubleStream。
流水线
在对流进行处理时,不同的流操作以级联的方式形成处理流水线。一个流水线由一个源(source),0 到多个中间操作(intermediate operation)和一个终结操作(terminal operation)完成。
- 源:源是流中元素的来源。Java 提供了很多内置的源,包括数组、集合、生成函数和 I/O 通道等。
- 中间操作:中间操作在一个流上进行操作,返回结果是一个新的流。这些操作是延迟执行的。
- 终结操作:终结操作遍历流来产生一个结果或是副作用。在一个流上执行终结操作之后,该流被消费,无法再次被消费。
流的处理流水线在其终结操作运行时才开始执行。
源
Java 8 支持从不同的源中创建流。Stream.of 方法可以使用给定的元素创建一个顺序流。使用 java.util.Arrays 的静态方法可以从数组中创建流,如清单5 所示。
清单 5. 从数组中创建流
Arrays.stream(new String[] {"Hello", "World"})
.forEach(System.out::println); // 输出"Hello\nWorld"到控制台
int sum = Arrays.stream(new int[] {1, 2, 3})
.reduce((a, b) -> a + b)
.getAsInt(); // "sum"的值是"6"
接口 Collection 的默认方法 stream() 和 parallelStream() 可以分别从集合中创建顺序流和并行流,如清单 6 所示。
清单 6. 从集合中创建流
List<String> list = new ArrayList<>();
list.add("Hello");
list.add("World");
list.stream()
.forEach(System.out::println); // 输出 Hello 和 World
中间操作
流中间操作在应用到流上,返回一个新的流。下面列出了常用的流中间操作:
- map:通过一个 Function 把一个元素类型为 T 的流转换成元素类型为 R 的流。
- flatMap:通过一个 Function 把一个元素类型为 T 的流中的每个元素转换成一个元素类型为 R 的流,再把这些转换之后的流合并。
- filter:过滤流中的元素,只保留满足由 Predicate 所指定的条件的元素。
- distinct:使用 equals 方法来删除流中的重复元素。
- limit:截断流使其最多只包含指定数量的元素。
- skip:返回一个新的流,并跳过原始流中的前 N 个元素。
- sorted:对流进行排序。
- peek:返回的流与原始流相同。当原始流中的元素被消费时,会首先调用 peek 方法中指定的 Consumer 实现对元素进行处理。
- dropWhile:从原始流起始位置开始删除满足指定 Predicate 的元素,直到遇到第一个不满足 Predicate 的元素。
- takeWhile:从原始流起始位置开始保留满足指定 Predicate 的元素,直到遇到第一个不满足 Predicate 的元素。
在清单 7 中,第一段代码展示了 flatMap 的用法,第二段代码展示了 takeWhile 和 dropWhile 的用法。
清单 7. 中间操作示例
Stream.of(1, 2, 3)
.map(v -> v + 1)
.flatMap(v -> Stream.of(v * 5, v * 10))
.forEach(System.out::println); //输出 10,20,15,30,20,40
Stream.of(1, 2, 3)
.takeWhile(v -> v < 3)
.dropWhile(v -> v < 2)
.forEach(System.out::println); //输出 2
终结操作
终结操作产生最终的结果或副作用。下面是一些常见的终结操作。
forEach 和 forEachOrdered 对流中的每个元素执行由 Consumer 给定的实现。在使用 forEach 时,并没有确定的处理元素的顺序;forEachOrdered 则按照流的相遇顺序来处理元素,如果流有确定的相遇顺序的话。
reduce 操作把一个流约简成单个结果。约简操作可以有 3 个部分组成:
- 初始值:在对元素为空的流进行约简操作时,返回值为初始值。
- 叠加器:接受 2 个参数的 BiFunction。第一个参数是当前的约简值,第二个参数是当前元素,返回结果是新的约简值。
- 合并器:对于并行流来说,约简操作可能在流的不同部分上并行执行。合并器用来把部分约简结果合并为最终的结果。
在清单 8 中,第一个 reduce 操作是最简单的形式,只需要声明叠加器即可。初始值是流的第一个元素;第二个 reduce 操作提供了初始值和叠加器;第三个 reduce 操作声明了初始值、叠加器和合并器。
清单 8. reduce 操 作示例
Stream.of(1, 2, 3).reduce((v1, v2) -> v1 + v2)
.ifPresent(System.out::println); // 输出 6
int result1 = Stream.of(1, 2, 3, 4, 5)
.reduce(1, (v1, v2) -> v1 * v2);
System.out.println(result1); // 输出 120
int result2 = Stream.of(1, 2, 3, 4, 5)
.parallel()
.reduce(0, (v1, v2) -> v1 + v2, (v1, v2) -> v1 + v2);
System.out.println(result2); // 输出 15
Max 和 min 是两种特殊的约简操作,分别求得流中元素的最大值和最小值。
对于一个流,操作 allMatch、anyMatch 和 nonMatch 分别用来检查是否流中的全部元素、任意元素或没有元素满足给定的条件。判断的条件由 Predicate 指定。
操作 findFirst 和 findAny 分别查找流中的第一个或任意一个元素。两个方法的返回值都是 Optional 对象。当流为空时,返回的是空的 Optional 对象。如果一个流没有确定的相遇顺序,那么 findFirst 和 findAny 的行为在本质上是相同的。
操作 collect 表示的是另外一类的约简操作。与 reduce 不同在于,collect 会把结果收集到可变的容器中,如 List 或 Set。收集操作通过接口 java.util.stream.Collector 来实现。Java 已经在类 Collectors 中提供了很多常用的 Collector 实现。
第一类收集操作是收集到集合中,常见的方法有 toList()、toSet() 和 toMap() 等。第二类收集操作是分组收集,即使用 groupingBy 对流中元素进行分组。分组时对流中所有元素应用同一个 Function。具有相同结果的元素被分到同一组。分组之后的结果是一个 Map,Map 的键是应用 Function 之后的结果,而对应的值是属于该组的所有元素的 List。在清单 9 中,流中的元素按照字符串的第一个字母分组,所得到的 Map 中的键是 A、B 和 D,而 A 对应的 List 值中包含了 Alex 和 Amy 两个元素,B 和 D 所对应的 List 值则只包含一个元素。
清单 9. 收集器 groupingBy 示 例
final Map<Character, List<String>> names = Stream.of("Alex", "Bob", "David", "Amy")
.collect(Collectors.groupingBy(v -> v.charAt(0)));
System.out.println(names);
第三类的 joining 操作只对元素类型为 CharSequence 的流使用,其作用是把流中的字符串连接起来。清单 10 中把字符串流用”, “进行连接。
清单 10. 收集器 joining 示 例
String str = Stream.of("a", "b", "c")
.collect(Collectors.joining(", "));
System.out.println(str);
第四类的 partitioningBy 操作的作用类似于 groupingBy,只不过分组时使用的是 Predicate,也就是说元素最多分成两组。所得到结果的 Map 的键的类型是 Boolean,而值的类型同样是 List。
还有一些收集器可以进行数学计算,不过只对元素类型为 int、long 或 double 的流可用。这些数学计算包括:
averagingDouble、averagingInt 和 averagingLong 计算流中元素的平均值。 summingDouble、summingInt 和 summingLong 计算流中元素的和。 summarizingDouble、summarizingInt 和 summarizingLong 对流中元素进行数学统计,可以得到平均值、数量、和、最大值和最小值。
清单 11 展示了这些数学计算相关的收集器的用法。
清单 11. 与数学计算相关的收集器
double avgLength = Stream.of("hello", "world", "a")
.collect(Collectors.averagingInt(String::length));
System.out.println(avgLength);
final IntSummaryStatistics statistics = Stream.of("a", "b", "cd")
.collect(Collectors.summarizingInt(String::length));
System.out.println(statistics.getAverage());
System.out.println(statistics.getCount());
Stream 中还有其他实用的操作,限于篇幅不能全部介绍。相关的用法可以查看 API 文档。
总结3
Java 8 引入的 Lambda 表达式和流处理是可以极大提高开发效率的重要特性。每个 Java 开发人员都应该熟练掌握它们的使用。本文从 JSR 335 出发对 Lambda 表达式进行了深入的介绍,同时也对流的特征和操作进行了详细说明。下一篇文章将对 Java 平台上流行的函数式编程库 Vavr 进行介绍。
参考资源3
- 参考关于 Lambda 表达式的 JSR 335 的内容。
- 查看 JDK 10 中 Stream 的相关文档 。
- 查看 JDK 10 中的 Spliterator 相关文档 。
4、使用Vavr进行函数式编程
原文地址4
前言4
在本系列的上一篇文章中对 Java 平台提供的 Lambda 表达式和流做了介绍。受限于 Java 标准库的通用性要求和二进制文件大小,Java 标准库对函数式编程的 API 支持相对比较有限。函数的声明只提供了 Function 和 BiFunction 两种,流上所支持的操作的数量也较少。为了更好地进行函数式编程,我们需要第三方库的支持。Vavr 是 Java 平台上函数式编程库中的佼佼者。
Vavr 这个名字对很多开发人员可能比较陌生。它的前身 Javaslang 可能更为大家所熟悉。Vavr 作为一个标准的 Java 库,使用起来很简单。只需要添加对 io.vavr:vavr 库的 Maven 依赖即可。Vavr 需要 Java 8 及以上版本的支持。本文基于 Vavr 0.9.2 版本,示例代码基于 Java 10。
元组
元组(Tuple)是固定数量的不同类型的元素的组合。元组与集合的不同之处在于,元组中的元素类型可以是不同的,而且数量固定。元组的好处在于可以把多个元素作为一个单元传递。如果一个方法需要返回多个值,可以把这多个值作为元组返回,而不需要创建额外的类来表示。根据元素数量的不同,Vavr 总共提供了 Tuple0、Tuple1 到 Tuple8 等 9 个类。每个元组类都需要声明其元素类型。如 Tuple2<String, Integer>表示的是两个元素的元组,第一个元素的类型为 String,第二个元素的类型为 Integer。对于元组对象,可以使用 _1、_2 到 _8 来访问其中的元素。所有元组对象都是不可变的,在创建之后不能更改。
元组通过接口 Tuple 的静态方法 of 来创建。元组类也提供了一些方法对它们进行操作。由于元组是不可变的,所有相关的操作都返回一个新的元组对象。在 清单 1 中,使用 Tuple.of 创建了一个 Tuple2 对象。Tuple2 的 map 方法用来转换元组中的每个元素,返回新的元组对象。而 apply 方法则把元组转换成单个值。其他元组类也有类似的方法。除了 map 方法之外,还有 map1、map2、map3 等方法来转换第 N 个元素;update1、update2 和 update3 等方法用来更新单个元素。
清单 1. 使用元组
Tuple2<String, Integer> tuple2 = Tuple.of("Hello", 100);
Tuple2<String, Integer> updatedTuple2 = tuple2.map(String::toUpperCase, v -> v * 5);
String result = updatedTuple2.apply((str, number) -> String.join(", ",
str, number.toString()));
System.out.println(result);
虽然元组使用起来很方便,但是不宜滥用,尤其是元素数量超过 3 个的元组。当元组的元素数量过多时,很难明确地记住每个元素的位置和含义,从而使得代码的可读性变差。这个时候使用 Java 类是更好的选择。
函数
Java 8 中只提供了接受一个参数的 Function 和接受 2 个参数的 BiFunction。Vavr 提供了函数式接口 Function0、Function1 到 Function8,可以描述最多接受 8 个参数的函数。这些接口的方法 apply 不能抛出异常。如果需要抛出异常,可以使用对应的接口 CheckedFunction0、CheckedFunction1 到 CheckedFunction8。
Vavr 的函数支持一些常见特征。
组合
函数的组合指的是用一个函数的执行结果作为参数,来调用另外一个函数所得到的新函数。比如 f 是从 x 到 y 的函数,g 是从 y 到 z 的函数,那么 g(f(x))是从 x 到 z 的函数。Vavr 的函数式接口提供了默认方法 andThen 把当前函数与另外一个 Function 表示的函数进行组合。Vavr 的 Function1 还提供了一个默认方法 compose 来在当前函数执行之前执行另外一个 Function 表示的函数。
在清单 2 中,第一个 function3 进行简单的数学计算,并使用 andThen 把 function3 的结果乘以 100。第二个 function1 从 String 的 toUpperCase 方法创建而来,并使用 compose 方法与 Object 的 toString 方法先进行组合。得到的方法对任何 Object 先调用 toString,再调用 toUpperCase。
清单 2. 函数的组合
Function3< Integer, Integer, Integer, Integer> function3 = (v1, v2, v3) -> (v1 + v2) * v3;
Function3< Integer, Integer, Integer, Integer> composed =
function3.andThen(v -> v * 100);
int result = composed.apply(1, 2, 3);
System.out.println(result);
// 输出结果 900
Function1< String, String> function1 = String::toUpperCase;
Function1< Object, String> toUpperCase = function1.compose(Object::toString);
String str = toUpperCase.apply(List.of("a", "b"));
System.out.println(str);
// 输出结果[A, B]
部分应用
在 Vavr 中,函数的 apply 方法可以应用不同数量的参数。如果提供的参数数量小于函数所声明的参数数量(通过 arity() 方法获取),那么所得到的结果是另外一个函数,其所需的参数数量是剩余未指定值的参数的数量。在清单 3 中,Function4 接受 4 个参数,在 apply 调用时只提供了 2 个参数,得到的结果是一个 Function2 对象。
清单 3. 函数的部分应用
Function4< Integer, Integer, Integer, Integer, Integer> function4 = (v1, v2, v3, v4) -> (v1 + v2) * (v3 + v4);
Function2< Integer, Integer, Integer> function2 = function4.apply(1, 2);
int result = function2.apply(4, 5);
System.out.println(result);
// 输出 27
柯里化方法
使用 curried 方法可以得到当前函数的柯里化版本。由于柯里化之后的函数只有一个参数,curried 的返回值都是 Function1 对象。在清单 4 中,对于 function3,在第一次的 curried 方法调用得到 Function1 之后,通过 apply 来为第一个参数应用值。以此类推,通过 3 次的 curried 和 apply 调用,把全部 3 个参数都应用值。
清单 4. 函数的柯里化
Function3<Integer, Integer, Integer, Integer> function3 = (v1, v2, v3) -> (v1 + v2) * v3;
int result = function3.curried().apply(1).curried().apply(2).curried().apply(3);
System.out.println(result);
记忆化方法
使用记忆化的函数会根据参数值来缓存之前计算的结果。对于同样的参数值,再次的调用会返回缓存的值,而不需要再次计算。这是一种典型的以空间换时间的策略。可以使用记忆化的前提是函数有引用透明性。
在清单 5 中,原始的函数实现中使用 BigInteger 的 pow 方法来计算乘方。使用 memoized 方法可以得到该函数的记忆化版本。接着使用同样的参数调用两次并记录下时间。从结果可以看出来,第二次的函数调用的时间非常短,因为直接从缓存中获取结果。
清单 5. 函数的记忆化
Function2<BigInteger, Integer, BigInteger> pow = BigInteger::pow;
Function2<BigInteger, Integer, BigInteger> memoized = pow.memoized();
long start = System.currentTimeMillis();
memoized.apply(BigInteger.valueOf(1024), 1024);
long end1 = System.currentTimeMillis();
memoized.apply(BigInteger.valueOf(1024), 1024);
long end2 = System.currentTimeMillis();
System.out.printf("%d ms -> %d ms", end1 - start, end2 - end1);
注意,memoized 方法只是把原始的函数当成一个黑盒子,并不会修改函数的内部实现。因此,memoized 并不适用于直接封装本系列第二篇文章中用递归方式计算斐波那契数列的函数。这是因为在函数的内部实现中,调用的仍然是没有记忆化的函数。
值
Vavr 中提供了一些不同类型的值。
Option
Vavr 中的 Option 与 Java 8 中的 Optional 是相似的。不过 Vavr 的 Option 是一个接口,有两个实现类 Option.Some 和 Option.None,分别对应有值和无值两种情况。使用 Option.some 方法可以创建包含给定值的 Some 对象,而 Option.none 可以获取到 None 对象的实例。Option 也支持常用的 map、flatMap 和 filter 等操作,如清单 6 所示。
清单 6. 使用 Option 的示例
Option<String> str = Option.of("Hello");
str.map(String::length);
str.flatMap(v -> Option.of(v.length()));
Either
Either 表示可能有两种不同类型的值,分别称为左值或右值。只能是其中的一种情况。Either 通常用来表示成功或失败两种情况。惯例是把成功的值作为右值,而失败的值作为左值。可以在 Either 上添加应用于左值或右值的计算。应用于右值的计算只有在 Either 包含右值时才生效,对左值也是同理。
在清单 7 中,根据随机的布尔值来创建包含左值或右值的 Either 对象。Either 的 map 和 mapLeft 方法分别对右值和左值进行计算。
清单 7. 使用 Either 的示例
import io.vavr.control.Either;
import java.util.concurrent.ThreadLocalRandom;
public class Eithers {
private static ThreadLocalRandom random = ThreadLocalRandom.current();
public static void main(String[] args) {
Either<String, String> either = compute()
.map(str -> str + " World")
.mapLeft(Throwable::getMessage);
System.out.println(either);
}
private static Either<Throwable, String> compute() {
return random.nextBoolean()
? Either.left(new RuntimeException("Boom!"))
: Either.right("Hello");
}
}
Try
Try 用来表示一个可能产生异常的计算。Try 接口有两个实现类,Try.Success 和 Try.Failure,分别表示成功和失败的情况。Try.Success 封装了计算成功时的返回值,而 Try.Failure 则封装了计算失败时的 Throwable 对象。Try 的实例可以从接口 CheckedFunction0、Callable、Runnable 或 Supplier 中创建。Try 也提供了 map 和 filter 等方法。值得一提的是 Try 的 recover 方法,可以在出现错误时根据异常进行恢复。
在清单 8 中,第一个 Try 表示的是 1/0 的结果,显然是异常结果。使用 recover 来返回 1。第二个 Try 表示的是读取文件的结果。由于文件不存在,Try 表示的也是异常。
清单 8. 使用 Try 的示例
Try<Integer> result = Try.of(() -> 1 / 0).recover(e -> 1);
System.out.println(result);
Try<String> lines = Try.of(() -> Files.readAllLines(Paths.get("1.txt")))
.map(list -> String.join(",", list))
.andThen((Consumer<String>) System.out::println);
System.out.println(lines);
Lazy
Lazy 表示的是一个延迟计算的值。在第一次访问时才会进行求值操作,而且该值只会计算一次。之后的访问操作获取的是缓存的值。在清单 9 中,Lazy.of 从接口 Supplier 中创建 Lazy 对象。方法 isEvaluated 可以判断 Lazy 对象是否已经被求值。
清单 9. 使用 Lazy 的示例
Lazy<BigInteger> lazy = Lazy.of(() ->
BigInteger.valueOf(1024).pow(1024));
System.out.println(lazy.isEvaluated());
System.out.println(lazy.get());
System.out.println(lazy.isEvaluated());
数据结构
Vavr 重新在 Iterable 的基础上实现了自己的集合框架。Vavr 的集合框架侧重在不可变上。Vavr 的集合类在使用上比 Java 流更简洁。
Vavr 的 Stream 提供了比 Java 中 Stream 更多的操作。可以使用 Stream.ofAll 从 Iterable 对象中创建出 Vavr 的 Stream。下面是一些 Vavr 中添加的实用操作:
groupBy:使用 Fuction 对元素进行分组。结果是一个 Map,Map 的键是分组的函数的结果,而值则是包含了同一组中全部元素的 Stream。 partition:使用 Predicate 对元素进行分组。结果是包含 2 个 Stream 的 Tuple2。Tuple2 的第一个 Stream 的元素满足 Predicate 所指定的条件,第二个 Stream 的元素不满足 Predicate 所指定的条件。 scanLeft 和 scanRight:分别按照从左到右或从右到左的顺序在元素上调用 Function,并累积结果。 zip:把 Stream 和一个 Iterable 对象合并起来,返回的结果 Stream 中包含 Tuple2 对象。Tuple2 对象的两个元素分别来自 Stream 和 Iterable 对象。 在清单 10 中,第一个 groupBy 操作把 Stream 分成奇数和偶数两组;第二个 partition 操作把 Stream 分成大于 2 和不大于 2 两组;第三个 scanLeft 对包含字符串的 Stream 按照字符串长度进行累积;最后一个 zip 操作合并两个流,所得的结果 Stream 的元素数量与长度最小的输入流相同。
清单 10. Stream 的使用示例
Map<Boolean, List<Integer>> booleanListMap = Stream.ofAll(1, 2, 3, 4, 5)
.groupBy(v -> v % 2 == 0)
.mapValues(Value::toList);
System.out.println(booleanListMap);
// 输出 LinkedHashMap((false, List(1, 3, 5)), (true, List(2, 4)))
Tuple2<List<Integer>, List<Integer>> listTuple2 = Stream.ofAll(1, 2, 3, 4)
.partition(v -> v > 2)
.map(Value::toList, Value::toList);
System.out.println(listTuple2);
// 输出 (List(3, 4), List(1, 2))
List<Integer> integers = Stream.ofAll(List.of("Hello", "World", "a"))
.scanLeft(0, (sum, str) -> sum + str.length())
.toList();
System.out.println(integers);
// 输出 List(0, 5, 10, 11)
List<Tuple2<Integer, String>> tuple2List = Stream.ofAll(1, 2, 3)
.zip(List.of("a", "b"))
.toList();
System.out.println(tuple2List);
// 输出 List((1, a), (2, b))
Vavr 提供了常用的数据结构的实现,包括 List、Set、Map、Seq、Queue、Tree 和 TreeMap 等。这些数据结构的用法与 Java 标准库的对应实现是相似的,但是提供的操作更多,使用起来也更方便。在 Java 中,如果需要对一个 List 的元素进行 map 操作,需要使用 stream 方法来先转换为一个 Stream,再使用 map 操作,最后再通过收集器 Collectors.toList 来转换回 List。而在 Vavr 中,List 本身就提供了 map 操作。清单 11 中展示了这两种使用方式的区别。
清单 11. Vavr 中数据结构的用法
List.of(1, 2, 3).map(v -> v + 10); //Vavr
java.util.List.of(1, 2, 3).stream()
.map(v -> v + 10).collect(Collectors.toList()); //Java 中 Stream
模式匹配
在 Java 中,我们可以使用 switch 和 case 来根据值的不同来执行不同的逻辑。不过 switch 和 case 提供的功能很弱,只能进行相等匹配。Vavr 提供了模式匹配的 API,可以对多种情况进行匹配和执行相应的逻辑。在清单 12 中,我们使用 Vavr 的 Match 和 Case 替换了 Java 中的 switch 和 case。Match 的参数是需要进行匹配的值。Case 的第一个参数是匹配的条件,用 Predicate 来表示;第二个参数是匹配满足时的值。$(value) 表示值为 value 的相等匹配,而 $() 表示的是默认匹配,相当于 switch 中的 default。
清单 12. 模式匹配的示例
String input = "g";
String result = Match(input).of(
Case($("g"), "good"),
Case($("b"), "bad"),
Case($(), "unknown")
);
System.out.println(result);
// 输出 good
在清单 13 中,我们用 $(v -> v > 0) 创建了一个值大于 0 的 Predicate。这里匹配的结果不是具体的值,而是通过 run 方法来产生副作用。
清单 13. 使用模式匹配来产生副作用
int value = -1;
Match(value).of(
Case($(v -> v > 0), o -> run(() -> System.out.println("> 0"))),
Case($(0), o -> run(() -> System.out.println("0"))),
Case($(), o -> run(() -> System.out.println("< 0")))
);
// 输出< 0
总结4
当需要在 Java 平台上进行复杂的函数式编程时,Java 标准库所提供的支持已经不能满足需求。Vavr 作为 Java 平台上流行的函数式编程库,可以满足不同的需求。本文对 Vavr 提供的元组、函数、值、数据结构和模式匹配进行了详细的介绍。下一篇文章将介绍函数式编程中的重要概念 Monad。
参考资源4
- 参考 Vavr 的 官方文档 。
- 查看 Vavr 的 Java API 文档 。
5、深入解析Monad
原文地址5
前言5
在本系列的前四篇文章中对函数式编程进行了多方位的介绍。本文将着重介绍函数式编程中一个重要而又复杂的概念:Monad。一直以来,Monad 都是函数式编程中最具有神秘色彩的概念。正如 JSON 格式的提出者 Douglas Crockford 所指出的,Monad 有一种魔咒,一旦你真正理解了它的意义,就失去了解释给其他人的能力。本文尝试深入解析 Monad 这一概念。由于 Monad 的概念会涉及到一些数学理论,可能读起来会比较枯燥。本文侧重在 Monad 与编程相关的方面,并结合 Java 示例代码来进行说明。
范畴论
要解释 Monad,就必须提到范畴论(Category Theory)。范畴(category)本身是一个很简单的概念。一个范畴由对象(object)以及对象之间的箭头(arrow)组成。范畴的核心是组合,体现在箭头的组合性上。如果从对象 A 到对象 B 有一个箭头,从对象 B 到对象 C 也有一个箭头,那么必然有一个从对象 A 到对象 C 的箭头。从 A 到 C 的这个箭头,就是 A 到 B 的箭头和 B 到 C 的箭头的组合。这种组合的必然存在性,是范畴的核心特征。以专业术语来说,箭头被称为态射(morphisms)。范畴中对象和箭头的概念可以很容易地映射到函数中。类型可以作为范畴中的对象,把函数看成是箭头。如果有一个函数 f 的参数类型是 A,返回值类型是 B,那么这个函数是从 A 到 B 的态射;另外一个函数 g 的参数类型是 B,返回值类型是 C,这个函数是从 B 到 C 的态射。可以把 f 和 g 组合起来,得到一个新的从类型 A 到类型 C 的函数,记为 g ∘f,也就是从 A 到 C 的态射。这种函数的组合方式是必然存在的。
一个范畴中的组合需要满足两个条件:
- 组合必须是传递的(associative)。如果有 3 个态射 f、g 和 h 可以按照 h∘g∘f 的顺序组合,那么不管是 g 和 h 先组合,还是 f 和 g 先组合,所产生的结果都是一样的。
- 对于每个对象 A,都有一个作为组合基本单元的箭头。这个箭头的起始和终止都是该对象 A 本身。当该箭头与从对象 A 起始或结束的其他箭头组合时,得到的结果是原始的箭头。以函数的概念来说,这个函数称为恒等函数(identity function)。在 Java 中,这个函数由 Function.identity() 表示。
从编程的角度来说,范畴论的概念要求在设计时应该考虑对象的接口,而不是具体的实现。范畴论中的对象非常的抽象,没有关于对象的任何定义。我们只知道对象上的箭头,而对于对象本身则一无所知。对象实际上是由它们之间的相互组合关系来定义的。
范畴的概念虽然抽象,实际上也很容易找到现实的例子。最直接的例子是从有向图中创建出范畴。对于有向图中的每个节点,首先添加一个从当前节点到自身的箭头。然后对于每两条首尾相接的边,添加一条新的箭头连接起始和结束节点。如此反复,就得到了一个范畴。
范畴中的对象和态射的概念很抽象。从编程的角度来说,我们可以找到更好的表达方式。在程序中,讨论单个的对象实例并没有意义,更重要的是对象的类型。在各种编程语言中,我们已经认识了很多类型,包括 int、long、double 和 char 等。类型可以看成是值的集合。比如 bool 类型就只有两个值 true 和 false,int 类型包含所有的整数。类型的值可以是有限的,也可以是无限的。比如 String 类型的值是无限的。编程语言中的函数其实是从类型到类型的映射。对于参数超过 1 个的函数,总是可以使用柯里化来转换为只有一个参数的函数。
类型和函数可以分别与范畴中的对象和态射相对应。范畴中的对象是类型,而态射则是函数。类型的作用在于限定了范畴中态射可以组合的方式,也就是函数的组合方式。只有一个函数的返回值类型与另一个函数的参数类型匹配时,这两个函数才能并肯定可以组合。这也就满足了范畴的定义。
之前讨论的函数都是纯函数,不含任何副作用。而在实际的编程中,是离不开副作用的。纯函数适合于描述计算,但是没办法描述输出字符串到控制台或是写数据到文件这样的副作用。Monad 的作用正是解决了如何描述副作用的问题。实际上,纯粹的函数式编程语言 Haskell 正是用 Monad 来处理描述 IO 等基于副作用的操作。在介绍 Monad 之前,需要先说明 Functor。
Functor
Functor 是范畴之间的映射。对于两个范畴 A 和 B,Functor F 把范畴 A 中的对象映射到范畴 B 中。Functor 在映射时会保留对象之间的连接关系。如果范畴 A 中存在从对象 a 到对象 b 的态射,那么 a 和 b 经过 Functor F 在范畴 B 中的映射值 F a 和 F b 之间也存在着态射。同样的,态射之间的组合关系,以及恒等态射都会被保留。所以说 Functor 不仅是范畴中对象之间的映射,也是态射之间的映射。如果一个 Functor 从一个范畴映射到自己,称为 endofunctor。
前面提到过,编程语言中的范畴中的对象是类型,而态射是函数。因此,这样的 endofunctor 是从类型到类型的映射,同时也是函数到函数的映射。我们首先看一个具体的 Functor :Option。Option 的定义很简单,Java 标准库和 Vavr 中都有对应的类。不过我们这里讨论的 Option 与 Java 中的 Optional 类有很大不同。Option 本身是一个类型构造器,使用时需要提供一个类型,所得到的结果是另外一个新的类型。这里可以与 Java 中的泛型作为类比。Option 有两种可能的值:Some 和 None。Some 表示对应类型的一个值,而 None 表示没有值。对于一个从 a 到 b 的映射 f,可以很容易地找到与之对应的使用 Option 的映射。该映射把 None 对应到 None,而把 f(Some a)映射到 Some f(a)。
Monad
Monad 本身也是一种 Functor。Monad 的目的在于描述副作用。
函数的副作用与组合方式
清单 1 给出了一个简单的函数 increase。该函数的作用是返回输入的参数加 1 之后的值。除了进行计算之外,还通过 count++来修改一个变量的值。这行语句的出现,使得函数 increase 不再是纯函数,每次调用都会对外部环境造成影响。
清单 1. 包含副作用的函数
int count = 0;
int increase(int x) {
count++;
return x + 1;
}
清单 1 中的函数 increase 可以划分成两个部分:产生副作用的 count++,以及剩余的不产生副作用的部分。如果可以通过一些转换,把副作用从函数 increase 中剥离出来,那么就可以得到另外一个纯函数的版本 increase1,如清单 2 所示。对函数 increase1 来说,我们可以把返回值改成一个 Vavr 中的 Tuple2<Integer, Integer> 类型,分别包含函数原始的返回值 x + 1 和在 counter 上增加的增量值 1。通过这样的转换之后,函数 increase1 就变成了一个纯函数。
清单 2. 转换之后的纯函数版本
Tuple2<Integer, Integer> increase1(int x) {
return Tuple.of(x + 1, 1);
}
在经过这样的转换之后,对于函数 increase1 的调用方式也发生了变化,如清单 3 所示。递增之后的值需要从 Tuple2 中获取,而 count 也需要通过 Tuple2 的值来更新。
清单 3. 调用转换之后的纯函数版本
int x = 0;
Tuple2<Integer, Integer> result = increase1(x);
x = result._1;
count += result._2;
我们可以采用同样的方式对另外一个相似的函数 decrease 做转换,如清单 4 所示。
清单 4. 函数 decrease 及其纯函数版本
int decrease(int x) {
count++;
return x - 1;
}
Tuple2<Integer, Integer> decrease1(int x) {
return Tuple.of(x - 1, 1);
}
不过需要注意的是,经过这样的转换之后,函数的组合方式发生了变化。对于之前的 increase 和 decrease 函数,可以直接组合,因为它们的参数和返回值类型是匹配的,如类似 increase(decrease(x)) 或是 decrease(increase(x)) 这样的组合方式。而经过转换之后的 increase1 和 decrease1,由于返回值类型改变,increase1 和 decrease1 不能按照之前的方式进行组合。函数 increase1 的返回值类型与 decrease1 的参数类型不匹配。对于这两个函数,需要另外的方式来组合。
在清单 5 中,compose 方法把两个类型为 Function<Integer, Tuple2<Integer, Integer>> 的函数 func1 和 func2 进行组合,返回结果是另外一个类型为 Function<Integer, Tuple2<Integer, Integer>> 的函数。在进行组合时,Tuple2 的第一个元素是实际需要返回的结果,按照纯函数组合的方式来进行,也就是把 func1 调用结果的 Tuple2 的第一个元素作为输入参数来调用 func2。Tuple2 的第二个元素是对 count 的增量。需要把这两个增量相加,作为 compose 方法返回的 Tuple2 的第二个元素。
清单 5. 函数的组合方式
Function<Integer, Tuple2<Integer, Integer>> compose(
Function<Integer, Tuple2<Integer, Integer>> func1,
Function<Integer, Tuple2<Integer, Integer>> func2) {
return x -> {
Tuple2<Integer, Integer> result1 = func1.apply(x);
Tuple2<Integer, Integer> result2 = func2.apply(result1._1);
return Tuple.of(result2._1, result1._2 + result2._2);
};
}
清单 6 中的 doCompose 函数对 increase1 和 decrease1 进行组合。对于一个输入 x,由于 increase1 和 decrease1 的作用相互抵消,得到的结果是值为 (x, 2) 的对象。
清单 6. 函数组合示例
Tuple2<Integer, Integer> doCompose(int x) {
return compose(this::increase1, this::decrease1).apply(x);
}
可以看到,doCompose 函数的输入参数和返回值类型与 increase1 和 decrease1 相同。所返回的结果可以继续使用 doCompose 函数来与其他类型相同的函数进行组合。
Monad 的定义
现在回到函数 increase 和 decrease。从范畴论的角度出发,我们考虑下面一个范畴。该范畴中的对象仍然是 int 和 bool 等类型,但是其中的态射不再是简单的如 increase 和 decrease 这样的函数,而是把这些函数通过类似从 increase 到 increase1 这样的方式转换之后的函数。范畴中的态射必须是可以组合的,而这些函数的组合是通过调用类似 doCompose 这样的函数完成的。这样就满足了范畴的第一条原则。而第二条原则也很容易满足,只需要把参数 x 的值设为 0,就可以得到组合的基本单元。由此可以得出,我们定义了一个新的范畴,而这个范畴就叫做 Kleisli 范畴。每个 Kleisli 范畴所使用的函数转换方式是独特的。清单 2 中的示例使用 Tuple2 来保存 count 的增量。与之对应的,Kleisli 范畴中对态射的组合方式也是独特的,类似清单 6 中的 doCompose 函数。
在对 Kleisli 范畴有了一个直观的了解之后,就可以对 Monad 给出一个形式化的定义。给定一个范畴 C 和 endofunctor m,与之相对应的 Kleisli 范畴中的对象与范畴 C 相同,但态射是不同的。K 中的两个对象 a 和 b 之间的态射,是由范畴 C 中的 a 到 m(b) 的态射来实现的。注意,Kleisli 范畴 K 中的态射箭头是从对象 a 到对象 b 的,而不是从对象 a 到 m(b)。如果存在一种传递的组合方式,并且每个对象都有组合单元箭头,也就是满足范畴的两大原则,那么这个 endofunctor m 就叫做 Monad。
一个 Monad 的定义中包含了 3 个要素。在定义 Monad 时需要提供一个类型构造器 M 和两个操作 unit 和 bind:
- 类型构造器的作用是从底层的类型中创建出一元类型(monadic type)。如果 M 是 Monad 的名称,而 t 是数据类型,则 M t 是对应的一元类型。
- unit 操作把一个普通值 t 通过类型构造器封装在一个容器中,所产生的值的类型是 M t。unit 操作也称为 return 操作。return 操作的名称来源于 Haskell。不过由于 return 在很多编程语言中是保留关键词,用 unit 做名称更为合适。
- bind 操作的类型声明是 (M t)→(t→M u)→(M u)。该操作接受类型为 M t 的值和类型为 t → M u 的函数来对值进行转换。在进行转换时,bind 操作把原始值从容器中抽取出来,再应用给定的函数进行转换。函数的返回值是一个新的容器值 M u。M u 可以作为下一次转换的起点。多个 bind 操作可以级联起来,形成处理流水线。
如果只看 Monad 的定义,会有点晦涩难懂。实际上清单 2 中的示例就是一种常见的 Monad,称为 Writer Monad。下面我们结合 Java 代码来看几种常见的 Monad。
Writer Monad
清单 2 展示了 Writer Monad 的一种用法,也就是累积 count 的值。实际上,Writer Monad 的主要作用是在函数调用过程中收集辅助信息,比如日志信息或是性能计数器等。其基本的思想是把副作用中对外部环境的修改聚合起来,从而把副作用从函数中分离出来。聚合的方式取决于所产生的副作用。清单 2 中的副作用是修改计算器 count,相应的聚合方式是累加计数值。如果副作用是产生日志,相应的聚合方式是连接日志记录的字符串。聚合方式是每个 Writer Monad 的核心。对于聚合方式的要求和范畴中对于态射的要求是一样,也就是必须是传递的,而且有组合的基本单元。在清单 5 中,聚合方式是 Integer 类型的相加操作,是传递的;同时也有基本单元,也就是加零。
下面对 Writer Monad 进行更加形式化的说明。Writer Monad 除了其本身的类型 T 之外,还有另外一个辅助类型 W,用来表示聚合值。对类型 W 的要求是前面提到的两点,也就是存在传递的组合操作和基本单元。Writer Monad 的 unit 操作比较简单,返回的是类型 T 的值 t 和类型 W 的基本单元。而 bind 操作则需要分别转换类型 T 和 W 的值。对于 T 的值,按照 Monad 自身的定义来转换;而对于 W 的值,则使用该类型的传递操作来聚合值。聚合的结果作为转换之后的新的 W 的值。
清单 7 中是记录日志的 Writer Monad 的实例。该 Monad 自身的类型使用 Java 泛型类型 T 来表示,而辅助类型是 List<String>,用来保存记录的日志。List<String> 满足作为辅助类型的要求。List<String> 上的相加操作是传递的,也存在作为基本单元的空列表。LoggingMonad 中的 unit 方法返回传入的值 value 和空列表。bind 方法的第一个参数是 LoggingMonad<T1> 类型,作为变换的输入;第二个参数是 Function<T1, LoggingMonad<T2>> 类型,用来把类型 T1 转换成新的 LoggingMonad<T2> 类型。辅助类型 List<String> 中的值通过列表相加的方式进行组合。方法 pipeline 表示一个处理流水线,对于一个输入 Monad,依次应用指定的变换,得到最终的结果。在使用示例中,LoggingMonad 中封装的是 Integer 类型,第一个转换把值乘以 4,第二个变换把值除以 2。每个变换都记录自己的日志。在运行流水线之后,得到的结果包含了转换之后的值和聚合的日志。
清单 7. 记录日志的 Monad
public class LoggingMonad<T> {
private final T value;
private final List<String> logs;
public LoggingMonad(T value, List<String> logs) {
this.value = value;
this.logs = logs;
}
@Override
public String toString() {
return "LoggingMonad{" +
"value=" + value +
", logs=" + logs +
'}';
}
public static <T> LoggingMonad<T> unit(T value) {
return new LoggingMonad<>(value, List.of());
}
public static <T1, T2> LoggingMonad<T2> bind(LoggingMonad<T1> input, Function<T1, LoggingMonad<T2>> transform) {
final LoggingMonad<T2> result = transform.apply(input.value);
List<String> logs = new ArrayList<>(input.logs);
logs.addAll(result.logs);
return new LoggingMonad<>(result.value, logs);
}
public static <T> LoggingMonad<T> pipeline(LoggingMonad<T> monad, List<Function<T, LoggingMonad<T>>> transforms) {
LoggingMonad<T> result = monad;
for (Function<T, LoggingMonad<T>> transform : transforms) {
result = bind(result, transform);
}
return result;
}
public static void main(String[] args) {
Function<Integer, LoggingMonad<Integer>> transform1 = v -> new LoggingMonad<>(v * 4, List.of(v + " * 4"));
Function<Integer, LoggingMonad<Integer>> transform2 = v -> new LoggingMonad<>(v / 2, List.of(v + " / 2"));
final LoggingMonad<Integer> result = pipeline(LoggingMonad.unit(8),
List.of(transform1, transform2));
System.out.println(result); // 输出为 LoggingMonad{value=16, logs=[8 * 4, 32 / 2]}
}
}
Reader Monad
Reader Monad 也被称为 Environment Monad,描述的是依赖共享环境的计算。Reader Monad 的类型构造器从类型 T 中创建出一元类型 E → T,而 E 是环境的类型。类型构造器把类型 T 转换成一个从类型 E 到 T 的函数。Reader Monad 的 unit 操作把类型 T 的值 t 转换成一个永远返回 t 的函数,而忽略类型为 E 的参数;bind 操作在转换时,在所返回的函数的函数体中对类型 T 的值 t 进行转换,同时保持函数的结构不变。
清单 8 是 Reader Monad 的示例。Function<E, T> 是一元类型的声明。ReaderMonad 的 unit 方法返回的 Function 只是简单的返回参数值 value。而 bind 方法的第一个参数是一元类型 Function<E, T1>,第二个参数是把类型 T1 转换成 Function<E, T2> 的函数,返回值是另外一个一元类型 Function<E, T2>。bind 方法的转换逻辑首先通过 input.apply(e) 来得到类型为 T1 的值,再使用 transform.apply 来得到类型为 Function<E, T2» 的值,最后使用 apply(e) 来得到类型为 T2 的值。
清单 8. Reader Monad 示例
public class ReaderMonad {
public static <T, E> Function<E, T> unit(T value) {
return e -> value;
}
public static <T1, T2, E> Function<E, T2> bind(Function<E, T1> input, Function<T1, Function<E, T2>> transform) {
return e -> transform.apply(input.apply(e)).apply(e);
}
public static void main(String[] args) {
Function<Environment, String> m1 = unit("Hello");
Function<Environment, String> m2 = bind(m1, value -> e -> e.getPrefix() + value);
Function<Environment, Integer> m3 = bind(m2, value -> e -> e.getBase() + value.length());
int result = m3.apply(new Environment());
System.out.println(result);
}
}
清单 8 中使用的环境类型 Environment 如清单 9 所示,其中有两个方法 getPrefix 和 getBase 分别返回相应的值。清单 8 的 m1 是值为 Hello 的单元类型,m2 使用了 Environment 的 getPrefix 方法进行转换,而 m3 使用了 getBase 方法进行转换,最终输出的结果是 107。因为字符串 Hello 在添加了前缀 $$ 之后的长度是 7,与 100 相加之后的值是 107。
清单 9. 环境类型
public class Environment {
public String getPrefix() {
return "$$";
}
public int getBase() {
return 100;
}
}
State Monad
State Monad 可以在计算中附加任意类型的状态值。State Monad 与 Reader Monad 相似,只是 State Monad 在转换时会返回一个新的状态对象,从而可以描述可变的环境。State Monad 的类型构造器从类型 T 中创建一个函数类型,该函数类型的参数是状态对象的类型 S,而返回值包含类型 S 和 T 的值。State Monad 的 unit 操作返回的函数只是简单地返回输入的类型 S 的值;bind 操作所返回的函数类型负责在执行时传递正确的状态对象。
清单 10 给出了 State Monad 的示例。State Monad 使用元组 Tuple2<T, S> 来保存计算值和状态对象,所对应的一元类型是 Function<S, Tuple2<T, S» 表示的函数。unit 方法所返回的函数只是简单地返回输入状态对象。bind 方法的转换逻辑使用 input.apply(s) 得到 T1 和 S 的值,再用得到的 S 值调用 transform。
清单 10. State Monad 示例
public class StateMonad {
public static <T, S> Function<S, Tuple2<T, S>> unit(T value) {
return s -> Tuple.of(value, s);
}
public static <T1, T2, S> Function<S, Tuple2<T2, S>> bind(Function<S, Tuple2<T1, S>> input,
Function<T1, Function<S, Tuple2<T2, S>>> transform) {
return s -> {
Tuple2<T1, S> result = input.apply(s);
return transform.apply(result._1).apply(result._2);
};
}
public static void main(String[] args) {
Function<String, Function<String, Function<State, Tuple2<String, State>>>> transform =
prefix -> value -> s -> Tuple .of(prefix + value, new State(s.getValue() + value.length()));
Function<State, Tuple2<String, State>> m1 = unit("Hello");
Function<State, Tuple2<String, State>> m2 = bind(m1, transform.apply("1"));
Function<State, Tuple2<String, State>> m3 = bind(m2, transform.apply("2"));
Tuple2<String, State> result = m3.apply(new State(0));
System.out.println(result);
}
}
State Monad 中使用的状态对象如清单 11 所示。State 是一个包含值 value 的不可变对象。清单 10 中的 m1 封装了值 Hello。transform 方法用来从输入的字符串前缀 prefix 中创建转换函数。转换函数会在字符串值上添加给定的前缀,同时会把字符串的长度进行累加。转换函数每次都返回一个新的 State 对象。转换之后的结果中字符串的值是 21Hello,而 State 对象中的 value 为 11,是字符串 Hello 和 1Hello 的长度相加的结果。
清单 11. 状态对象
public class State {
private final int value;
public State(final int value) {
this.value = value;
}
public int getValue() {
return value;
}
@Override
public String toString() {
return "State{" +
"value=" + value +
'}';
}
}
总结5
作为本系列的最后一篇文章,本文对函数式编程中的重要概念 Monad 做了详细的介绍。本文从范畴论出发,介绍了使用 Monad 描述函数副作用的动机和方式,以及 Monad 的定义。本文还对常见的几种 Monad 进行了介绍,并添加了相应的 Java 代码。
参考资源5
- 阅读 Category Theory for Programmers 一书来深入理解范畴论。
- 了解更多关于 Monad 的内容。
- 了解 Java 中的 Functor 和 Monad 。
- 了解 Haskell 中的更多 Monad 类型。